Scaling laws for wave energy dissipation in microscopic fracture
Under moderate pressures, when two materials are in contact they fuse together at a small number of contact points. When forced to slide past each other the contact points eventually fail and this cycle of stick-slip produces sudden rapid local accelerations at the point of contact. In the crust of the earth, an earthquake is born.
Studying earthquakes experimentally at full scale is obviously impossible, so seismologists and people interested in frictional processes have tried studying "acoustic emissions" (high frequency waves coming from small scale sliding) in tabletop scale sliding experiments where all the variables can be controlled.
One issue of interest to these studies is the detectability of small events. When only a small piece of material slides, waves will carry relatively little total energy. As the wave spreads over a spherical wavefront the energy density decreases like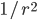 
and dissipates. But also we expect such small scale waves to couple to the thermal vibrations within the material and dissipate according to different scaling laws in this additional process. Both processes can result in the waves dissipating before they reach our detector if the initial energy is small enough.
To isolate the thermal effect from geometric spreading and scattering effects, we studied waves induced in a long thin bar of simulated molecules on a computer. In this case wave spreading over a spherical front is not an issue, and energy is perfectly conserved. Nevertheless the wave rapidly dampens down after just a few passes through the bar. Depending on the size of the bar and the temperature of the material, different decay rates are observed. How can we make sense of the thermally induced decay rate?
As part of his PhD dissertation Daniel Lakeland investigated this phenomenon and came up with results that closely track the detailed 3D molecular dynamics simulations. The key insight was that within a macroscopic region containing multiple molecules, the energy available to the molecules near the boundary of the region controls how much pressure the region exerts on its neighbors, and is related to both the thermal energy within the region and via thermal mixing, to the center of mass translational wave energy. The coupling constant comes from a ratio of timescales being the timescale for a thermal fluctuation (1 molecular time unit) to the timescale for thermal diffusion from the center of the region to the edge (via a random walk). In very small regions, a correction is required for the finite-range interactions between molecules. Incorporating these results into a simple ODE and fitting the constant coefficient via statistical methods led to remarkably accurate results.
Using this ratio of times as the scaling law for the coefficient in front of a momentum diffusion term added to the standard elastic wave equation accounts for the rate of decay of wave energy observed in the full 3D molecular dynamics analysis over a wide range of size and temperature scales. This research is fully documented in the PhD dissertation, and is currently being prepared for publication in a peer reviewed physics or mechanics journal.